Topological systems
3D topological insulators are a new phase of quantum matter with a strong spin-orbit coupling. They exhibit insulating behaviour in the bulk while surface states lead to metallic conduction at the surfaces only. The surface states offer an unusual spin-polarized band structure not seen before. The two linear dispersion branches with opposite spins are protected by time reversal symmetry and cross at the Dirac point. However, this symmetry can be broken by introducing atomic spins (e.g. Co), which was theoretically predicted to cause a gap opening at the Dirac point. Topologically ordered phases of matter are extremely rare, the most well known example is the quantum Hall phase, which is realized in a two-dimensional electron system in a large external magnetic field. In topological insulators, intrinsic spin-orbit coupling simulates the effect of a spin-dependent external magnetic field, leading to quantum Hall-like effect without any external magnetic field. Usually topological insulators are studied by angle resolved photoemission spectroscopy in order to reveal the band structure which allows to detect the topological order. This is due to the fact that topological insulators exhibit no quantized transport response and cannot be observed by means of a transport measurement. Topological protected surface states were experimentally recently discovered in HgTe, Bi2Se3, Bi2Te3 , Bi1-xSbx alloys, or Sb(0001) and still further efforts are made in order to find other materials which reveal these unique properties.
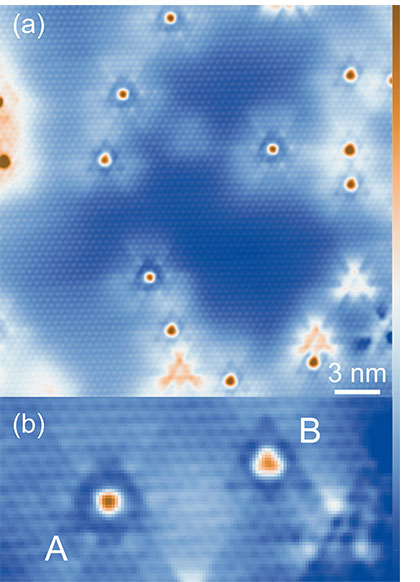
Figure: As an example for atomic spins on the surface of a 3D topological insulator, the figure shows a constant current image of individual iron atoms adsorbed on the surface of Bi2Se3. The iron atoms adsorb on the two different hollow sites of the surface selenium lattice (A and B). We collaborate with different research groups in order to complement our STS investigations of such systems by angle resolved photoemission spectroscopy, x-ray magnetic circular dichroism measurements, and density-functional theory calculations.
