Noncollinear Spins

Non-collinear magnetic order

Magnetism in low-dimensions is a fascinating topic: Even in apparently simple systems such as monolayers the nearest neighbor distance, the symmetry and the hybridization with the substrate can play a crucial role for the magnetic properties. This may lead to a variety of magnetic structures, from the ferromagnetic and antiferromagnetic state to complex, non-collinear spin textures. While the formation of a ferromagnetic or antiferromagnetic state can be the result of a dominating nearest neighbor exchange interaction, complex magnetic structures often reflect a situation of competing magnetic interactions. Magnetic interactions in a monolayer on a substrate can be described by mapping the results of ab-initio electronic structure calculations on a two-dimensional classical Heisenberg model. This makes it possible to search for the origin of a specific magnetic ground state, i.e. to find out which interactions dominate or compete. This of course facilitates a general understanding of magnetism and might allow the tailoring of magnetic properties in the future.

 

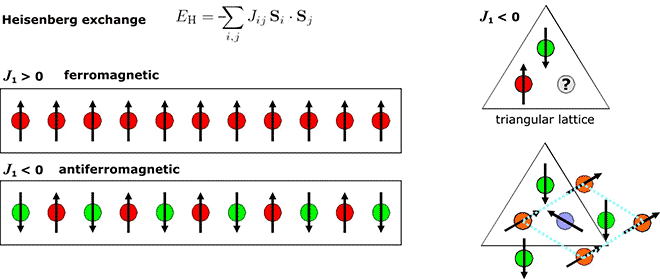
A fundamental magnetic interaction between atomic spins S is the Heisenberg exchange. Depending on the sign of the nearest neighbor interaction J1 the ground state is ferromagnetic or antiferromagnetic. However, on a triangular lattice a negative J1 leads to geometrical frustration and the non-collinear 120°-Neel state is favored.

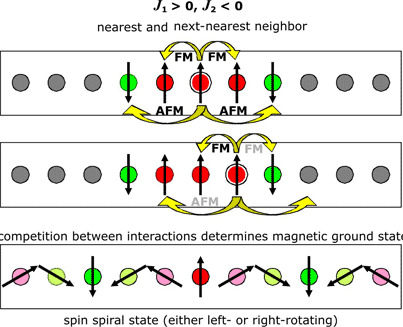
When the second-nearest neighbor interaction is on the same order as the first this may lead to frustration and a homogeneous spin spiral can be the magnetic ground state. Since J is isotropic the spin spiral can rotate either in one direction or the other, and it may be helical or cycloidal.

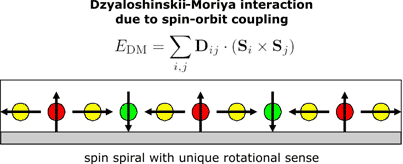
The Dzyaloshinskii-Moriya (DM) interaction links the spins via a vector product and may play a role when the inversion symmetry is broken, which is always the case at surfaces. It favors a 90°-spin spiral and the rotational sense is determined by the sign of D; high symmetry surfaces typically lead to cycloidal spin spirals. Of course competition between Heisenberg exchange and DM-interaction may lead to spin spirals with any angle between adjacent spins and also higher-order interactions can play a role for the magnetic ground state.

Spin-polarized scanning tunneling microscopy (SP-STM) combines magnetic sensitivity with high lateral resolution and therefore grants access to complex magnetic order with unit cells on the nanometer scale. Different previously inconceivable magnetic structures are observed in pseudomorphic 3d monolayers on late 5d transition metal substrates [1-6]:

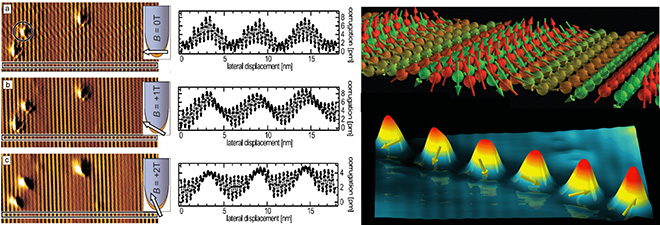
The first spin spiral ground state at a surface was observed in the system of one monolayer of Mn on a W(110) surface [1]. Due to the competition of antiferromagnetic nearest neighbor Heisenberg exchange and DM interaction adjacent spins enclose an angle of ~170°, resulting in a nanometer-sized magnetic period. Since this state does not have a net magnetic moment in the magnetic unit cell it does not respond to an external magnetic field. However, in an SP-STM experiment a ferromagnetic tip can be aligned in an external magnetic field and thereby different magnetic components of the sample can be probed at different magnetic fields. The combined information of these experiments proves the spin spiral order. When single Co atoms are deposited on this cycloidal spin spiral (bottom right) they couple ferromagnetically to the adjacent Mn atoms, thus mimicking the spin spiral order depending on their exact position. In spin-resolved measurements this is directly reflected in the height and shape of the single Co atoms [2].


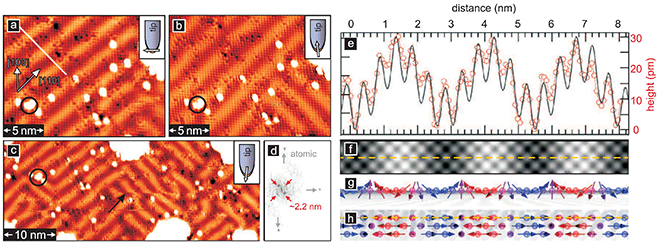
To study the influence of the symmetry of the atomic lattice on spin spiral states we investigated the pseudomorphic Mn monolayer on W(001) which has a four-fold symmetry. We again observe a cycloidal spin spiral in spin-resolved measurements [3] which has atoms with magnetization components in the surface plane (a) and normal to the surface (b). On a larger sized image (c) one can see a labyrinth pattern due to spin spirals propagating along the two equivalent directions of the surface, which gives rise to four spots in the Fourier transform of this image (d). Note that in addition to the magnetic signal we obtain atomic resolution for this sample system, which has proven to be very difficult for other systems studied so far. The experimental line profile indicated by the white line in (a) is shown in (e) as red open circles. The periodicity can be fitted to obtain a simulated SP-STM image (f). The underlying spin spiral is sketched as side (g) and top view (h) and ab-initio calculations have confirmed that it has a unique rotational sense due to the DM interaction.

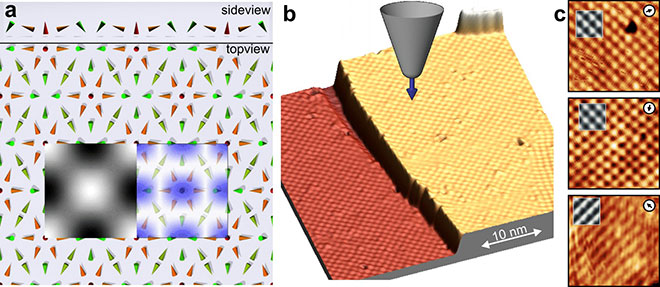
In contrast to the 1 dimensional spin spirals in the Mn monolayers on different W surfaces, the Fe monolayer on Ir(111) features a 2 dimensional magnetic state which can be described as a lattice of magnetic skyrmions. Skyrmions are topologically protected field configurations with particle-like properties that play an important role in various fields of science. The sketch on the left shows the square lattice of skyrmions which have a size of only 15 atoms. Using spin-polarized scanning tunnelling microscopy (middle) we can directly image this non-collinear spin texture in real space. Combining information about the out of-plane and three different in-plane magnetization components of the sample we can unambiguously identify a topologically protected magnetic ground state. With the aid of first-principles calculations, we develop a spin model on a discrete lattice that identifies the interplay of Heisenberg exchange, the four-spin and the Dzyaloshinskii–Moriya interaction as the microscopic origin of this magnetic state.