Graphene
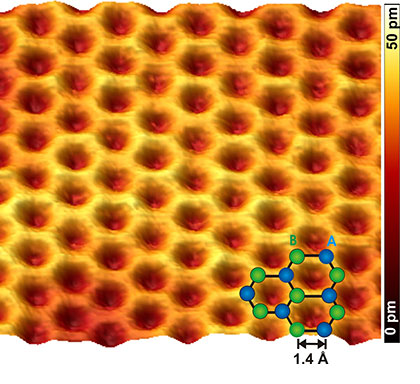
Fig. STM topography revealing atomically resolved graphene lattice. The blue and green spheres indicate two carbon atoms of the unit cell labeled by A and B. Tunneling parameters are I=10 pA and U=50mV.
Graphene is a monolayer of carbon atoms, which are arranged in a honeycomb lattice consisting of two equivalent triangular sublattices A and B. It is a truly two-dimensional crystal and is the basic component of the other carbon allotropes with a sp² hybridization, i.e. graphite (3D), nanotubes (1D), and fullerenes (0D). Graphene is unique in the sense that it exhibits mechanical properties of a flexible membrane and at the same time electronic properties of a zero band gap semiconductor that valence and conduction bands touch each other at the K point of the Brillouin zone (the so-called Dirac point). Near these points, the dispersion relation is linear in contrast to conventional metals or semiconductors where the energy spectrum is parabolic (free-electron-like). For this reason, graphene provides peculiar electronic properties which are not anymore described by the Schrödinger but the Dirac equation.Nowadays, this remarkable material is easily available, due to the development of synthesis methods such as mechanical exfoliation and epitaxial growth. Especially, in applied science, its transport properties are exploited. Since graphene exhibits an extremely high carrier mobility — larger than 1x105 cm2/Vs — and can be tuned between hole and electron conduction, it is an excellent candidate for possible applications in the next generation of electronic devices. Therefore it is crucial to understand the electronic properties of graphene depending on the interface between graphene and the supporting substrate. In particular, we are interested in its electronic properties as a function of the corrugation, thickness, and defects of graphene on metal substrates. Another main goal is the investigation of the interaction of graphene with magnetic or non-magnetic nanostructures (adatoms, intercalated atoms, defects, or clusters) in order to investigate the local properties of these nanoscale objects prepared on a truly two-dimensional system.
