Monte Carlo simulation
A Monte Carlo simulation is a stochastic method, which relies on repeated random experiments. This method is mainly used, if it is impossible or infeasible to compute an exact result. The calculated observables are statistical averages, whose variance strongly depends on the number of performed random samplings.
We use Monte Carlo simulations to model and predict the physical properties of our sample systems. Here, the energy and the spatially resolved magnetization of the simulated system are the for us most important observables. In a Monte Carlo simulation random states are created according to a predefined probability distribution. Depending on the problem, a suitable probability function has to be chosen, because it determines the trajectory the system traverse in phase space. An important characteristic of this method is, that the newly created states do not depend on the previous states, hence, the system does not have a memory. The repeated sampling of such states is called a Markov chain. By creating a Markov chain the discrete Monte Carlo algorithm satisfies the condition of detailed balance, which ensures, the system to relax into the canonical equilibrium. As in our group many different experiments are available, we can directly compare the results from simulations with real system. This combination between experimental and theoretical approaches allows further insight to the physical properties of the system under investigation. For further information and mathematical background of Monte Carlo simulations we refer to the literature [1].
Application
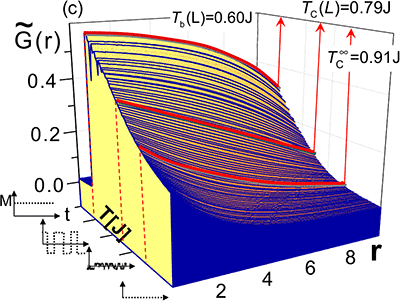
To increase the density of future magnetic storage devices the size of the magnetic bits, the carrier of the magnetic information, need to be decreased constantly. In our group we do not concentrate on the technical realization to shrink those bits, but to find the physical limits and to determine the technical limits, where the bit can still be controlled. The smaller the bit, the easier a bit is excited thermally. Hence, the smaller the bit, the smaller the temperature at which the magnetic information is lost. This phenomena is called superparamagnetism and is one of the biggest challenges for future storage technology. To define and understand the limits of superparamagnetism, we study the temperature region of the magnetic stability in dependence of the bit size [2], see figure 1. From Monte Carlo simulation we not only gain insight to the temperature dependent switching frequency, but also insight to the switching mechanism. By comparison between experiment and simulation, we could show, that even very small bits, consisting of less than 100 atoms, switch via nucleation and propagation of domain walls and not as assumed by coherent rotation [3].
Figure 1: By fitting the correlation function G(r), one can determine the critical temperatures.
In another study we propose a theoretical concept of domain wall manipulation by means of the tip of a spin-polarized scanning tunneling microscope and check our concept performing Monte Carlo simulations .The domain wall is driven by a spin-polarized current induced by the magnetic tip placed above the magnetic nanowire and then moved along its long axis with a current flowing through the vacuum barrier. The angular momentum coming from the spin-polarized current exerts a torque on the magnetic moments underneath the tip and leads to a displacement of the domain wall. By analyzing time-dependent Monte Carlo configurations , we can study the kinematics of the domain wall motion. Hence, we can observe how the systems relaxes into thermal equilibrium [4, Spin dynamic simulation]. Figure 2 shows an animation of a successful domain wall manipulation.

Figure 2: Animation of a successful domain wall manipulation.