Mean field theory (MFT)

The mean field theory or mean field approximation is one of the most famous and on the other hand one of the most underestimated theories in solid science.

Theories like Hartree-Fock, the Stoner model, and the RPA decoupling in the Green function theory base on the mean field approximation. Furthermore the Ginzburg-Landau theory is a mean field theory. The idea of the mean field theory is to replace the fluctuating fields coming from the inter- and intraparticle interactions by a nonfluctuating mean field.  As a consequence the mean field theory can be used to give a qualitative, however no quantitative description. Nevertheless, the mean field theory is exact in the limit of high dimensions (upper critical dimension) and in the case of strong long-range interactions.

For the classical Heisenberg model:




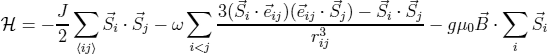
one has to replace the magnetic moment 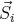   by 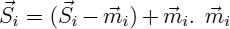   is the mean value of  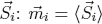. We get for  :




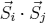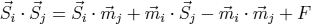
with the fluctuating term 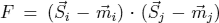 . In the mean field approximation we have to set  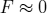. Furthermore, the last term  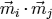  can be skipped. This term only scales the zero energy. Therefore, we get for the mean field Hamiltonian:




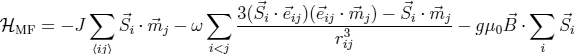
The magnetization can be calculated with:




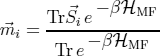
where 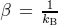 . Within the calculation  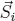  is given by spherical coordinates and the trace  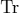 by the integration over the surface of an unit sphere:




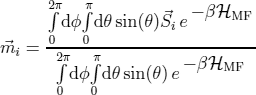
With this method we could show that near the Curie temperature 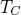   a deviation between the magnetization of a vortex core and the surrounding magnetization (domain) can be seen [1]. The vortex core magnetization shows a faster decrease than the magnetization of the domain. This means that additional to the thermal spin wave excitation and a superparamagnetic behavior of the vortex core longitudinal fluctuations near  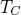  play a role. Fig. 1 shows the magnetization of vortex core and domain: Two different critical temperatures can be seen. The explanation is simple: Due to the reduced exchange and dipole-dipole interaction in the vortex core stronger fluctuations can be investigated leading to to a rapidly decrease of the magnetization. Within the mean field approximation the fluctuations are neglected, however the effect can be clearly seen. This mean that one can assume that the mean field theory underestimates this effect and reality a stronger deviation will be found.   

Furthermore, we have used the mean field approximation in our recent concerning the spin-spin correlation in ferromagnetic nanostructures [2]. However, it has been shown that the mean field theory fails in this case. The cause are the missing fluctuations.



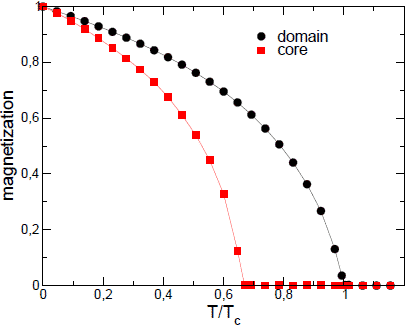
Fig.: Magnetization over temperature of a magnetic vortex: core = magnetization of the vortex core and domain = magnetization of the surrounding magnewtic moments.