Introduction to STM	Instrumentation	Projects
Gallery	Publications	Team

Implementation of temperature in micromagnetic simulations

theory | results | download

Micromagnetic theory

The usual way to simulate the evolution of a magnetic system is the cellwise numerical integration of the Landau-Lifshitz differential equation (LL)

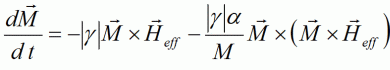
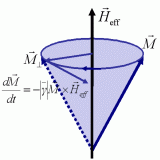where H_eff is an effective field, which represents all forces acting on the magnetic moment. A popular method to take temperature into account is adding a highly irregular fluctuating field h_fluct representing the irregular influence of temperature. The ordinary LL then becomes the stochastic Landau-Lifshitz differential equation (SLL).

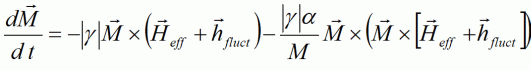
The most important parameters to be specified now, are the first two moments (mean and variance) of the fluctuating field h_fluct. The first moment <h_fluct> of course must be zero, since we shall not allow temperature to drive our system in a specific direction. Also it can be assumed, that the values of h_fluct follow a gaussian distribution because they arise from numerous interactions with the underlying crystal lattice. So for temperatures not too low the central limit theorem can be applied. Assuming a Boltzmann distribution in thermal equilibrium, the variance can be calculated to

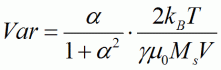
For most systems h_fluct can be looked upon as white noise with no correlation in time, space or axis direction. This will no longer hold for extremely low temperatures and/or extraordinary strong fields H_eff. For temperatures below 1K this model surely becomes questionable. Another important point is that stochastic functions are to be multiplied by 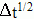not 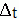like normal functions, when integrated numerically.

Introduction to STM | Instrumentation | Projects | Gallery | Publications | Team

impressum   © copyright 2002 by group R - university of hamburg